Мал. 2.8. Утворення негативних чисел різного розміру.

Такий спосіб утворення негативних чисел зручний тим, що дозволяє виконувати над ними арифметичні операції по загальних правилах з отриманням правильного результату. Так, складання чисел +5 і -5 дає 0; в результаті віднімання 3 з 5 виходить 2; віднімання -3 з -5 дає -2 і так далі
Аналізуючи алгоритм утворення негативного числа, можна відмітити, що для всіх негативних чисел характерна наявність двійкової одиниці в старшому біті. Позитивні числа, навпаки, мають в старшому біті 0. Це справедливо для чисел будь-якого розміру. Крім того, з мал. 2.8 видно, що для перетворення негативного 8-бітового числа в слово досить доповнити його зліва вісьма двійковими одиницями. Легко зміркувати, що для перетворення позитивного 8-бітового числа в слово його треба доповнити вісьма двійковими нулями. То ж справедливо і для перетворення слова із знаком в подвійне слово із знаком, тільки додати доведеться вже не 8, а 16 одиниць або нулів. У системі команд МП 86 і, відповідно, в мові асемблера, для цих операцій передбачені спеціальні команди cbw і cwd.
Слід підкреслити, що знак числа умовний. Одне і те ж число, наприклад, зображене на мал. 2.8 8-бітове число Fbh можна в одному контексті розглядати, як негативне (-5), а в іншому - як позитивне, або, правильніше, число без знаку (Fbh=251). Знак числа є характеристикою не самого числа, а нашого уявлення про його сенс.
На мал. 2.9 представлена вибіркова таблиця 16-бітових чисел з вказівкою їх машинного уявлення, а також значень без знаку і із знаком. З таблиці видно, що для чисел із знаком розміром в слово діапазон позитивних значень тягнеться від 0 до 32767, а діапазон негативних значень - від -1 до -32768.

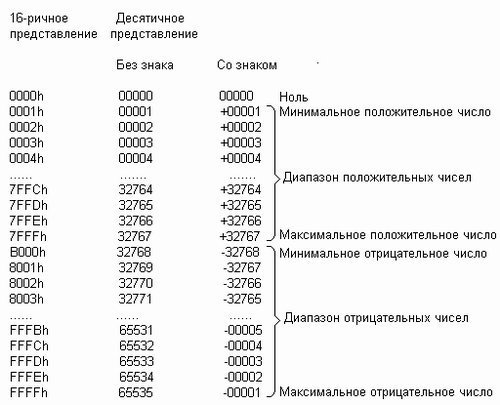
Мал. 2.9. Представлення 16-бітових чисел без знаку і із знаком.

На мал. 2.10 представлена аналогічна таблиця для 8-бітових чисел. З таблиці видно, що для чисел із знаком розміром в байт діапазон позитивних значень тягнеться від 0 до 127, а діапазон негативних значень - від -1 до -128.

Мал. 2.10. Представлення 8-бітових чисел без знаку і із знаком.

Серед команд процесора, що виконують ту або іншу обробку чисел, можна виділити команди, байдужі до знаку числа (наприклад, inc, add, test), команди, призначені для обробки чисел без знаку (mul, div, ja, jb і ін.), а також команди, спеціально розраховані на обробку чисел із знаком (imul, idiv, jg, jl і так далі). Особливості використання цих команд будуть описані в наступному розділі.
Розглянемо тепер інший вид представлення чисел - двійково-десятковий формат (binary-coded decimal, BCD), використовуваний у ряді прикладних областей. У такому форматі видають дані деякі вимірювальні прилади; він же використовується КМОП-ЧАСАМІ реального часу комп'ютерів IBM РС для зберігання інформації про поточний час. У МП 86 передбачений ряд команд для обробки таких чисел.
Двійково-десятковий формат існує в двох різновидах: упакований і розпакований. У першому випадку в байті записується дворозрядне десяткове число від 00 до 99. Кожна цифра числа займає половину байта і зберігається в двійковій формі. З мал. 2.11 можна відмітити, що для запису в байт десяткового числа в двійково-десятковому форматі досить супроводжувати записуване десяткове число символом h.

Мал. 2.11. Упакований двійково-десятковий формат.

У машинному слові або в 16-розрядному регістрі можна зберігати в двійково-десятковому форматі чотирирозрядні десяткові числа від 0000 9999 (ріс.2.12).

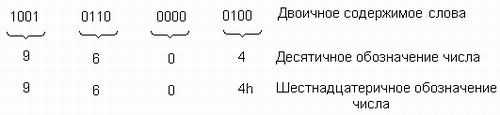
Мал. 2.12. Запис десяткового числа 9604 в слові.

Розпакований формат відрізняється від упакованого тим, що в кожному байті записується лише одна десяткова цифра (як і раніше в двійковій формі). В цьому випадку в слові можна записати десяткові числа від 00 99 (див. мал. 2.13)

Мал. 2.13. Запис десяткового числа 98 в розпакованому вигляді.